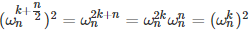Lvat_s Blog

一开始以为是一个高明的数据结构，后来发现直接拆式子就行了

举个$2*2$矩阵的例子

第一个矩阵

$$

 \begin{bmatrix}

 a_1 & a_2 \\

 a_3 & a_4 \\

 \end{bmatrix}

$$

第二个矩阵

$$

 \begin{bmatrix}

 b_1 & b_2 \\

 b_3 & b_4 \\

 \end{bmatrix}

$$

那么我们来乘一下，结果是

$$

 \begin{bmatrix}

 a_1*b_1+a_2*b_3 & a_2*b_4+a_1*b_2 \\

 a_3*b_1+a_4*b_3 & a_4*b_4+a_3*b_2 \\

 \end{bmatrix}

$$

加一下得到$a_1*(b_1+b_2)+a_2*(b_3+b_4)+a_3*(b_1+b_2)+a_4*(b_3+b_4)$

组合一下得到$(a_1+a_3)*(b_1+b_2)+(a_2+a_4)*(b_3*b_4)$

也就是第一个矩阵记录向上的前缀和，第二个矩阵记录向左的前缀和

然后乘一下就好了

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;

const register int N=2005;

static int n,m,a[N][N],b[N][N];

inline void Read(register int &x){
register char ch;
while((ch=getchar())<'0' || ch>'9');
x=ch-'0';
while((ch=getchar())>='0' && ch<='9')x=x*10+ch-'0';
}

int main(){
freopen("2901.in","r",stdin);
freopen("2901.out","w",stdout);
Read(n);Read(m);
for(register int i=1;i<=n;i++)for(register int j=1;j<=n;j++)Read(a[i][j]),a[i][j]+=a[i-1][j];
for(register int i=1;i<=n;i++)for(register int j=1;j<=n;j++)Read(b[i][j]),b[i][j]+=b[i][j-1];
while(m--){
	register int A,B,C,D;
	Read(A);Read(B);Read(C);Read(D);
	if(A>C)A^=C^=A^=C;
	if(B>D)B^=D^=B^=D;
	register long long ans=0;
    for(register int i=1;i<=n;i++)ans+=(1ll*a[C][i]-a[A-1][i])*(1ll*b[i][D]-b[i][B-1]);
    printf("%lld\n",ans);
}
return 0;
}

模拟即可

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;

int Dist2(int x,int y){
return x*x+y*y;
}

int test,n;

int main(){
freopen("4063.in","r",stdin);
freopen("4063.out","w",stdout);
scanf("%d",&test);
while(test--){
	long long ans=0;
	scanf("%d",&n);
    for(int i=1;i<=n;i++){
		int x,y;
        scanf("%d %d",&x,&y);
        int t=Dist2(x,y);
		if(t<=20*20){ans+=10;}
		else if(t<=40*40){ans+=9;}
		else if(t<=60*60){ans+=8;}
		else if(t<=80*80){ans+=7;}
		else if(t<=100*100){ans+=6;}
		else if(t<=120*120){ans+=5;}
		else if(t<=140*140){ans+=4;}
		else if(t<=160*160){ans+=3;}
        else if(t<=180*180){ans+=2;}
        else if(t<=200*200){ans+=1;}
    }
    printf("%lld\n",ans);
}
return 0;
}

模拟一下即可

注意适当的常数优化

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;

const int N=105,INF=2100000000;

int mp[N][N],mp2[N][N],n,m,ans=INF;

int Test(int r,int c){
int cnt=0;
for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)mp2[i][j]=mp[i][j];
for(int i=1;i+r-1<=n;i++){
	for(int j=1;j+c-1<=m;j++){
        if(mp2[i][j]){
			int tp=mp2[i][j];
			cnt+=tp;
            for(int k=1;k<=r;k++){
				for(int l=1;l<=c;l++){
                    mp2[i+k-1][j+l-1]-=tp;
                    if(mp2[i+k-1][j+l-1]<0)return INF;
				}
            }
        }
	}
}
for(int i=1;i<=n;i++){
	for(int j=1;j<=m;j++){
		if(mp2[i][j])return INF;
	}
}
return cnt;
}

int main(){
freopen("2241.in","r",stdin);
freopen("2241.out","w",stdout);
scanf("%d %d",&n,&m);
int tx=0;
for(int i=1;i<=n;i++){
	for(int j=1;j<=m;j++){
		scanf("%d",&mp[i][j]);tx+=mp[i][j];
	}
}
for(int r=1;r<=n;r++){
    for(int c=1;c<=m;c++){
		if(tx%(r*c) || tx/(r*c)+1>ans)continue;
        ans=min(ans,Test(r,c));
    }
}
printf("%d\n",ans);
return 0;
}

首先我们排个序，然后列一个dp方程

设$f[i][j]$为前i小的糖果至少匹配j个药片的数量

那么我们可以利用单调性把这个dp优化到$O(n^2)$

之后我们发现这个可能会重复统计

我们考虑怎么消除重复的部分

首先一个糖果匹配后面药片的总数为$n!$

然后其中重复统计的个数为之后计算的所有dp数组的值乘上一个组合数

那么我们倒着容斥就做完了

详见代码

#include<cstdio>
#include<algorithm>
using namespace std;

const int N=2005;
const long long P=1000000009ll;

int n,m,k;
long long a[N],b[N],C[N][N],fac[N],f[N][N];

int main(){
freopen("3622.in","r",stdin);
freopen("3622.out","w",stdout);
scanf("%d %d",&n,&m);
if((n+m)&1){puts("0");return 0;}
m=n+m>>1;
C[0][0]=fac[0]=f[0][0]=1;
for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
for(int i=1;i<=n;i++)scanf("%lld",&b[i]);
sort(a+1,a+n+1);sort(b+1,b+n+1);
for(int i=1;i<=n;i++){
	fac[i]=fac[i-1]*i%P;
	C[i][0]=C[i][i]=1;
	for(int j=1;j<i;j++)C[i][j]=(C[i-1][j]+C[i-1][j-1])%P;
}
for(int i=1;i<=n;i++){
	while(k<n && a[i]>b[k+1])k++;f[i][0]=1;
	for(int j=0;j<=i;j++)f[i][j]=(f[i-1][j]+f[i-1][j-1]*max(k-j+1,0))%P;
}
for(int i=n;i>=m;i--){
	f[n][i]=f[n][i]*fac[n-i]%P;
	for(int j=i+1;j<=n;j++){
		f[n][i]-=f[n][j]*C[j][i];
		f[n][i]=(f[n][i]+P)%P;
	}
}
printf("%lld\n",f[n][m]);
return 0;
}

类似虚树的东西

首先我们发现答案就是当前存在的点所构成的树的边权和的两倍

所以我们考虑用set维护dfs序，最后减掉一个lca(最前,最后)即可

具体为什么是这样么……你需要自己手动模拟一下

非常妙

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<set>
#include<algorithm>
using namespace std;

const int N=100005;
const long long INF=21000000000000ll;

int n,m,en,h[N],dep[N],pos[N],f[N],lg[N<<1],tag[N],Index,Size;
long long ans,d[N<<1][19],di[N];
set<int> St;

struct Edge{
int b,next;
long long v;
}e[N<<1];

void dfs(int u){
d[pos[u]=++Index][0]=di[u];
for(int i=h[u];i;i=e[i].next){
    int v=e[i].b;
    if(dep[v])continue;
    f[v]=u;
    di[v]=di[u]+e[i].v;
    dep[v]=dep[u]+1;
    dfs(v);
    d[++Index][0]=di[u];
}
}

template<typename T>inline void Read(T &x){char ch;while((ch=getchar())<'0'||ch>'9');x=ch-'0';while((ch=getchar())>='0'&&ch<='9')x=x*10+ch-'0';}
void AddEdge(int sa,int sb,long long sc){e[++en].b=sb;e[en].v=sc;e[en].next=h[sa];h[sa]=en;}
set<int>::iterator Pre(const set<int>::iterator &x){set<int>::iterator Tx=x;return --Tx;}
set<int>::iterator Nxt(const set<int>::iterator &x){set<int>::iterator Tx=x;return ++Tx;}
long long Mn(int u,int v){int w=lg[v-u+1];return min(d[u][w],d[v-(1<<w)+1][w]);}
long long Dist(){if(!Size)return 0ll;int u=*St.begin(),v=*Pre(St.end());return Mn(u,v);}

void Ins(int x){
ans+=d[x][0];
St.insert(x);
Size++;
if(Size==1)return;
set<int>::iterator Tx=St.find(x);
if(Tx==St.begin()){ans-=Mn(*Tx,*Nxt(Tx));return;}
if(Nxt(Tx)==St.end()){ans-=Mn(*Pre(Tx),*Tx);return;}
ans+=Mn(*Pre(Tx),*Nxt(Tx))-Mn(*Tx,*Nxt(Tx))-Mn(*Pre(Tx),*Tx);
}

void Del(int x){
ans-=d[x][0];
if(Size==1){St.erase(x);Size--;return;}
set<int>::iterator Tx=St.find(x);
if(Tx==St.begin()){ans+=Mn(*Tx,*Nxt(Tx));St.erase(x);Size--;return;}
if(Nxt(Tx)==St.end()){ans+=Mn(*Pre(Tx),*Tx);St.erase(x);Size--;return;}
ans-=Mn(*Pre(Tx),*Nxt(Tx))-Mn(*Tx,*Nxt(Tx))-Mn(*Pre(Tx),*Tx);
St.erase(x);
Size--;
}

int main(){
freopen("3991.in","r",stdin);
freopen("3991.out","w",stdout);
Read(n);Read(m);
for(int i=1;i<n;i++){
    int u,v;
    long long w;
    Read(u);Read(v);Read(w);
    AddEdge(u,v,w);
	AddEdge(v,u,w);
}
dfs(1);
for(int i=2;i<=Index;i++)lg[i]=lg[i>>1]+1;
for(int i=1;i<=lg[Index];i++)for(int j=1;j+(1<<i)-1<=Index;j++)d[j][i]=min(d[j][i-1],d[j+(1<<i-1)][i-1]);
for(int i=1;i<=m;i++){
    int x;
    Read(x);
    tag[x]^=1;
    if(tag[x])Ins(pos[x]);
    else Del(pos[x]);
    printf("%lld\n",ans-Dist()<<1);
}
return 0;
}

小伙伴们从四川回来了

5Au 4Ag 1Cu

lyz大爷高一随手Au，day2考246成功虐场

太强了%%%

而我在家连超哥线段树都不会（这两者有什么关系……）

还有好多坑没填

所以补一下

考虑标记永久化

计算断点位置对应的区间，确定怎么传标记

一开始我YY了一种写法，始终不过

后来发现情况少考虑了

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;

const int N=100005;

int n;
char s[10];
double ans;

struct SegTree{
int l,r;
double k,b;
inline double V(int x){return k*x+b;}
}tree[N<<2];

void Build(int rt,int l,int r){
tree[rt].l=l;
tree[rt].r=r;
tree[rt].k=tree[rt].b=0;
if(l==r)return;
int mid=l+r>>1;
Build(rt<<1,l,mid);
Build(rt<<1|1,mid+1,r);
}

double Cross(double k1,double b1,double k2,double b2){return (b2-b1)/(k1-k2);}

void Insert(int rt,double k,double b){
if(k*tree[rt].l+b<=tree[rt].V(tree[rt].l) && k*tree[rt].r+b<=tree[rt].V(tree[rt].r))return;
else if(k*tree[rt].l+b>=tree[rt].V(tree[rt].l) && k*tree[rt].r+b>=tree[rt].V(tree[rt].r)){tree[rt].k=k;tree[rt].b=b;return;}
int mid=tree[rt].l+tree[rt].r>>1;
double x=Cross(k,b,tree[rt].k,tree[rt].b);
if(k*tree[rt].l+b>=tree[rt].V(tree[rt].l)){
	if(x<=mid)Insert(rt<<1,k,b);
    else Insert(rt<<1|1,tree[rt].k,tree[rt].b),tree[rt].k=k,tree[rt].b=b;
}
else {
	if(x>mid)Insert(rt<<1|1,k,b);
    else Insert(rt<<1,tree[rt].k,tree[rt].b),tree[rt].k=k,tree[rt].b=b;
}
}

void Query(int rt,int x){
ans=max(ans,tree[rt].V(x));
if(tree[rt].l==tree[rt].r)return;
int mid=tree[rt].l+tree[rt].r>>1;
if(x<=mid)Query(rt<<1,x);
else Query(rt<<1|1,x);
}

int main(){
freopen("1568.in","r",stdin);
freopen("1568.out","w",stdout);
scanf("%d",&n);
Build(1,1,50000);
for(int i=1;i<=n;i++){
    scanf("%s",s);
    if(s[0]=='P'){double k,b;scanf("%lf %lf",&b,&k);Insert(1,k,b-k);}
    else {int x;scanf("%d",&x);ans=0;Query(1,x);printf("%lld\n",(long long)floor(ans/100.0));/*printf("%lf\n",ans);*/}
}
return 0;
}

先留下这个坑

这题我目前看到的有2种做法

做法1

做法2

占坑待填

教训：以后不能再取非常大的模数了，不然不好处理

最近因为某些原因没有更新博客……向还有在看我博客的人表示深深的歉意……

哈希，设dp[i][j]为第i个通配符的位置匹配了字符串前j位，转移基本是抄做法1的……

反正去不了绵阳了……

留下的好多的坑会一一填上。

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;

const int N=100005,M=15;
const long long P=1000000003ll,base=233ll;

bool f[M][N];
int n,len,pos[M],cnt;
long long Px[N]={1},ha1[N],ha2[N];
char s[N],str[N];

long long H1(int st,int ed){
if(st>ed)return 0ll;
return ((ha1[ed]-ha1[st-1]*Px[ed-st+1])%P+P)%P;
}

long long H2(int st,int ed){
if(st>ed)return 0ll;
return ((ha2[ed]-ha2[st-1]*Px[ed-st+1])%P+P)%P;
}

int main(){
freopen("3507.in","r",stdin);
freopen("3507.out","w",stdout);
scanf("%s",str+1);
len=strlen(str+1);
str[++len]='?';
for(int i=1;i<=len;i++)if(str[i]<'a' || str[i]>'z')pos[++cnt]=i;
for(int i=1;i<=len;i++)ha1[i]=ha1[i-1]*base%P+str[i];
for(int i=1;i<=100000;i++)Px[i]=Px[i-1]*base%P;
scanf("%d",&n);
while(n--){
	scanf("%s",s+1);
	len=strlen(s+1);
	s[++len]='#';
	for(int i=1;i<=len;i++)ha2[i]=ha2[i-1]*base%P+s[i];
    memset(f,0,sizeof(f));
    f[0][0]=1;
    for(int i=0;i<cnt;i++){
		if(str[pos[i]]=='*')for(int j=1;j<=len;j++)if(f[i][j-1])f[i][j]=1;
		for(int j=0;j<=len;j++){
            //printf("Ha1[%d,%d]=%lld , Ha2[%d,%d]=%lld\n",pos[i]+1,pos[i+1]-1,H1(pos[i]+1,pos[i+1]-1),j+1,j+pos[i+1]-pos[i]-1,H2(j+1,j+pos[i+1]-pos[i]-1));
			if(f[i][j]&&H1(pos[i]+1,pos[i+1]-1)==H2(j+1,j+pos[i+1]-pos[i]-1)){
				if(str[pos[i+1]]=='?')f[i+1][j+pos[i+1]-pos[i]]=1;
                else f[i+1][j+pos[i+1]-pos[i]-1]=1;
			}
		}
    }
    puts(f[cnt][len]?"YES":"NO");
}
return 0;
}

这是一篇简易的FFT教程，作者水平奇低无比，这篇博文仅仅是用于分享体会

已经学会FFT的神犇们可以直接无视这篇文章

推荐几个学习FFT的很好的博客地址:Picks大神的博客 Miskcoo大神的博客 FFT算法学习笔记 （对于想要进阶的来说去第一个，基础去第二个，入门去第三个）

我觉得学FFT先要去看上面三个博客，实在一点看不懂在看我的口胡……

而且我的口胡非常模糊(半夜三点在写这东西)，难免会出错，敬请指正~

嗯，蒟蒻Lvat_s开始口胡了

首先你需要知道什么是FFT

其实我也不知道是啥，但是有个专业的名字叫做Fast Fourier Transform(快速傅立叶变换)

相信看这篇博文的神犇们都具有初中数学姿势:一个二次函数可以被三个点表示出来

而小学数学告诉我们一个一次函数可以用两个点表示出来

所以，我们类比一下，一个n次多项式$F(n)=a_n*x^n+......+a_1*x+a_0$可以用n+1个二维平面上的点来表示，这些点称为多项式的点值表示法

我们再来思考一下函数是怎么乘起来的

例如$F*G=......$(懒得写了)(总之就是对于x坐标相同的点，将两个函数的y坐标值相乘后就行了)

那么对于点值表达我们可以$O(n)$的实现乘法

所以离散傅立叶变换(DFT)就是暴力的将这些点分拆与合并，时间复杂度$O(n^2)$

为什么DFT复杂度这么高？

都是开始分拆多项式和后期合并的锅!

初中数学告诉我们由一个二次函数得到的三个点不具有唯一性，而由三个点合成的那个二次函数一定是唯一的

我们再来类比一下就知道了n次多项式$F(n)$也可以这么做

所以，FFT就是找一些合适的点用$O(nlog_2n)$得到点值表达，然后$O(n)$计算乘法，最后用$O(nlog_2n)$来重新得到这个多项式。

然而怎么降低复杂度呢？

我们选择单位复数根的倍数作为我们要找的这些点的x坐标。

看起来好像一点用没有……真的没有吗？

当然是有用的了。

（未完待续）

更新啦

我们需要知道关于复数的两个引理

设$w_n=e^{2\pi/n}$

消去引理:$w_{dk}^{dk}=w_k^k(n>=0,k>=0,d>=0)$证明很简单，带进去算下就行= =

折半引理:我不太会Mathjax语法怎么办……那就弄个图片吧

还有一个求和引理就不发了= =懒得截图了

这三个引理使我们可以证明FFT的正确性。

FFT的核心就是分组(按照奇数和偶数对多项式的指数进行分组)。

如果我们可以在单次$O(n)$时间内合并($n$为多项式的长度)，那么多项式乘法就可以在$O(nlogn)$的时间内解决。

事实是确实可以这样

具体证明在我推荐的第三个博客地址里面就有，讲的还是很清晰的。

那么我们就可以递归FFT啦！

当然这样不优美。

我们可以改成非递归版的，这样节省时间。

写的好渣啊……主要是因为当初看了好多FFT方面的博客都看不懂，所以才决定事无巨细的写这篇文章。

====================分割线=======================

多项式求逆

这玩意要用到类似倍增的东西，我还没想太清楚……

过几天更新

orz rky大爷几个月前就会了

随机化乱搞

学习了一下bitset怎么用感觉不错

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<bitset>
#include<algorithm>
using namespace std;
 
const int N=105;
typedef bitset<N> Bt;
 
int n,d,ord[N],CNT=1000;
Bt A[N],nw,ans,can;
 
struct Point{
int x,y;
}poi[N];
 
int Sqr(int x){return x*x;}
int Dist(Point A,Point B){return Sqr(A.x-B.x)+Sqr(A.y-B.y);}
 
int main(){
freopen("4080.in","r",stdin);
freopen("4080.out","w",stdout);
scanf("%d %d",&n,&d);
for(int i=1;i<=n;i++)scanf("%d %d",&poi[i].x,&poi[i].y);
for(int i=1;i<=n;i++){
    for(int j=i+1;j<=n;j++){
        if(Dist(poi[i],poi[j])<=d*d)A[i].set(j),A[j].set(i);
    }
}
for(int i=1;i<=n;i++)ord[i]=i;
while(CNT--){
    can.set();
    nw.reset();
    for(int i=1;i<=n;i++){
        if(can.test(ord[i])){
            nw.set(ord[i]);
            can&=A[ord[i]];
        }
    }
    if(nw.count()>ans.count())ans=nw;
    random_shuffle(ord+1,ord+n+1);
}
printf("%d\n",ans.count());
for(int i=1;i<=n;i++)if(ans.test(i))printf("%d ",i);
return 0;
}

和我做过的另外一个BZOJ题很像，但是忘了题号了……BZOJ3306 题解

换根就是针对当前根找到子树然后容斥一下

注意dfs序中一棵树的子树一定是连续的

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
 
const int N=100005;
 
int n,m,a[N],id[N],pre[N],segn,en,h[N],root,siz[N],son[N],dep[N],fa[N],top[N],OPTION;
 
struct Edge{
int b,next;
}e[N<<1];
 
void AddEdge(int sa,int sb){
e[++en].b=sb;
e[en].next=h[sa];
h[sa]=en;
}
 
struct SegTree{
int l,r,mn,tag;
}tree[N<<2];
 
void Pushdown(int rt){
if(tree[rt].tag){
    tree[rt<<1].tag=tree[rt].tag;
    tree[rt<<1|1].tag=tree[rt].tag;
    tree[rt<<1].mn=tree[rt].tag;
    tree[rt<<1|1].mn=tree[rt].tag;
    tree[rt].tag=0;
}
}
 
void Pushup(int rt){
tree[rt].mn=min(tree[rt<<1].mn,tree[rt<<1|1].mn);
}
 
void Build(int rt,int l,int r){
tree[rt].l=l;tree[rt].r=r;
if(l==r){tree[rt].mn=a[pre[l]];return;}
int mid=l+r>>1;
Build(rt<<1,l,mid);
Build(rt<<1|1,mid+1,r);
Pushup(rt);
}
 
void Modify(int rt,int l,int r,int x){
if(l<=tree[rt].l && tree[rt].r<=r){tree[rt].mn=x;tree[rt].tag=x;return;}
Pushdown(rt);
int mid=tree[rt].l+tree[rt].r>>1;
if(l<=mid)Modify(rt<<1,l,r,x);
if(r>mid)Modify(rt<<1|1,l,r,x);
Pushup(rt);
}
 
int Query(int rt,int l,int r){
if(l<=tree[rt].l && tree[rt].r<=r)return tree[rt].mn;
Pushdown(rt);
int mid=tree[rt].l+tree[rt].r>>1;
if(r<=mid)return Query(rt<<1,l,r);
else if(l>mid)return Query(rt<<1|1,l,r);
else return min(Query(rt<<1,l,r),Query(rt<<1|1,l,r));
}
 
void dfs1(int u,int fat){
siz[u]=1;
dep[u]=dep[fat]+1;
son[u]=0;
fa[u]=fat;
for(int i=h[u];i;i=e[i].next){
    int v=e[i].b;
    if(v==fat)continue;
    dfs1(v,u);
    siz[u]+=siz[v];
    if(siz[v]>siz[son[u]])son[u]=v;
}
}
 
void dfs2(int u,int ux){
top[u]=ux;
id[u]=++segn;
pre[segn]=u;
if(son[u])dfs2(son[u],ux);
else return;
for(int i=h[u];i;i=e[i].next){
    int v=e[i].b;
    if(son[u]==v || fa[u]==v)continue;
    dfs2(v,v);
}
}
 
void Change(int x,int y,int v){
int topx=top[x],topy=top[y];
while(topx!=topy){
    if(dep[topx]<dep[topy]){swap(topx,topy);swap(x,y);}
    Modify(1,id[topx],id[x],v);
    x=fa[topx];
    topx=top[x];
}
if(dep[x]>dep[y])swap(x,y);
Modify(1,id[x],id[y],v);
}
 
int Ask(int Id){
if(root==Id)return Query(1,1,n);
int x=root,y=Id,topx=top[x],topy=top[y];
while(topx!=topy){
    if(dep[topx]<dep[topy]){swap(topx,topy);swap(x,y);}
    x=fa[topx];
    topx=top[x];
}
if(dep[x]>dep[y])swap(x,y);
if(x!=Id)return Query(1,id[Id],id[Id]+siz[Id]-1);
else {
    for(int i=h[Id];i;i=e[i].next){
        int v=e[i].b;
        if(fa[Id]==v)continue;
        if(id[v]<=id[root] && id[root]<=id[v]+siz[v]-1){
            int mn=Query(1,id[1],id[v]-1);
            if(id[v]+siz[v]-1!=n)mn=min(mn,Query(1,id[v]+siz[v],n));
            return mn;
        }
    }
}
}
 
void Read(int &x){
char ch;
while((ch=getchar())<'0' || ch>'9');
x=ch-'0';
while((ch=getchar())>='0' && ch<='9')x=x*10+ch-'0';
}
 
int main(){
freopen("3083.in","r",stdin);
freopen("3083.out","w",stdout);
Read(n);Read(m);
for(int i=1;i<n;i++){int u,v;Read(u);Read(v);AddEdge(u,v);AddEdge(v,u);}
for(int i=1;i<=n;i++)Read(a[i]);
Read(root);
dfs1(1,0);
dfs2(1,1);
Build(1,1,n);
while(m--){
    int opt,x,y,v;
    Read(opt);
    if(opt==1){Read(x);root=x;}
    if(opt==2){Read(x);Read(y);Read(v);Change(x,y,v);}
    if(opt==3){Read(x);printf("%d\n",Ask(x));}
}
return 0;
}