这是一篇简易的FFT教程,作者水平奇低无比,这篇博文仅仅是用于分享体会
已经学会FFT的神犇们可以直接无视这篇文章
推荐几个学习FFT的很好的博客地址:Picks大神的博客 Miskcoo大神的博客 FFT算法学习笔记 (对于想要进阶的来说去第一个,基础去第二个,入门去第三个)
我觉得学FFT先要去看上面三个博客,实在一点看不懂在看我的口胡……
而且我的口胡非常模糊(半夜三点在写这东西),难免会出错,敬请指正~
嗯,蒟蒻Lvat_s开始口胡了
首先你需要知道什么是FFT
其实我也不知道是啥,但是有个专业的名字叫做Fast Fourier Transform(快速傅立叶变换)
相信看这篇博文的神犇们都具有初中数学姿势:一个二次函数可以被三个点表示出来
而小学数学告诉我们一个一次函数可以用两个点表示出来
所以,我们类比一下,一个n次多项式$F(n)=a_n*x^n+......+a_1*x+a_0$可以用n+1个二维平面上的点来表示,这些点称为多项式的点值表示法
我们再来思考一下函数是怎么乘起来的
例如$F*G=......$(懒得写了)(总之就是对于x坐标相同的点,将两个函数的y坐标值相乘后就行了)
那么对于点值表达我们可以$O(n)$的实现乘法
所以离散傅立叶变换(DFT)就是暴力的将这些点分拆与合并,时间复杂度$O(n^2)$
为什么DFT复杂度这么高?
都是开始分拆多项式和后期合并的锅!
初中数学告诉我们由一个二次函数得到的三个点不具有唯一性,而由三个点合成的那个二次函数一定是唯一的
我们再来类比一下就知道了n次多项式$F(n)$也可以这么做
所以,FFT就是找一些合适的点用$O(nlog_2n)$得到点值表达,然后$O(n)$计算乘法,最后用$O(nlog_2n)$来重新得到这个多项式。
然而怎么降低复杂度呢?
我们选择单位复数根的倍数作为我们要找的这些点的x坐标。
看起来好像一点用没有……真的没有吗?
当然是有用的了。
(未完待续)
更新啦
我们需要知道关于复数的两个引理
设$w_n=e^{2\pi/n}$
消去引理:$w_{dk}^{dk}=w_k^k(n>=0,k>=0,d>=0)$证明很简单,带进去算下就行= =
折半引理:我不太会Mathjax语法怎么办……那就弄个图片吧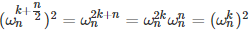
还有一个求和引理就不发了= =懒得截图了
这三个引理使我们可以证明FFT的正确性。
FFT的核心就是分组(按照奇数和偶数对多项式的指数进行分组)。
如果我们可以在单次$O(n)$时间内合并($n$为多项式的长度),那么多项式乘法就可以在$O(nlogn)$的时间内解决。
事实是确实可以这样
具体证明在我推荐的第三个博客地址里面就有,讲的还是很清晰的。
那么我们就可以递归FFT啦!
当然这样不优美。
我们可以改成非递归版的,这样节省时间。
写的好渣啊……主要是因为当初看了好多FFT方面的博客都看不懂,所以才决定事无巨细的写这篇文章。
====================分割线=======================
多项式求逆
这玩意要用到类似倍增的东西,我还没想太清楚……
过几天更新
orz rky大爷几个月前就会了
Jul 28, 2016 07:30:18 PM
楼主怎么不更了呀 ?
Jul 31, 2016 02:33:21 AM
@cooordi: 居然有人看我的博客……感动啊……
最近忙于学(颓)习(废)(当然我是没钱党,怎么可能玩守望),博客有一段时间没更了
我会在近几天把全部更完的:)
Jul 31, 2016 11:33:19 PM
加油咯博主! 最近在编个程要用fft,但是之前没学过所以好多概念都不太懂...T_T...