一道反演的好题
首先我们需要推一下式子（写在纸上发现不太好写在电脑上）
拍照太烦了……其实就是Claris博客上的公式
然后倒数第二行那个式子的前缀和我不太会。。本来想问Claris的后来自己推了一下就会了
网上题解都好玄学啊
首先对于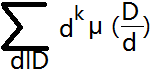
这么一个式子(用画图画的请见谅……我不会LateX)
我们把这个式子的值用一个函数F(D)表示
然后我们可以发现:对于D为质数，那么d只有两个值：一个是1，一个是D
那么我们可以暴力快速幂乘起来就可以了
如果D不是质数，为了简化我们假设这个D可以由两个质数相乘
那么d的取值可以是:1,第一个质数，第二个质数，两个质数之积
那么我们设f[i]=i是质数则为ik,否则为0
g[i]=这个和数会由哪些质数组成
我们就可得到F[i*pri[j]]=F[pri[j]]*F[i],因为这个F[i*pri[j]]会由F[i]和F[i*pri[j]]组成,那么两个sigma相乘自然就是这个值了
对于两个质数以上的乘积我觉得和上面一样的。。主要分g[i]是否等于i(i是质数)和g[i]不等于i两种情况考虑，就可以了
#include<cstdio>
#include<cstdlib>
#include<algorithm>
using namespace std;
const int N=5000000,Mod=1000000007;
int T,n,m,k,pri[N/5+1],mu[N+5],tab[N+5],g[N+5],sum[N+5],F[N+5],f[N+5],cnt;
int Pow(int x,int y){
int base=x,ans=1;
while(y){
if(y&1)ans=1ll*ans*base%Mod;
base=1ll*base*base%Mod;
y>>=1;
}
return ans;
}
void Prepare(){
mu[1]=1;
F[1]=1;
for(int i=2;i<=N;i++){
if(!tab[i]){pri[++cnt]=i;mu[i]=-1;f[i]=Pow(i,k);F[i]=f[i]-1;g[i]=i;}
for(int j=1;j<=cnt && i*pri[j]<=N;j++){
tab[pri[j]*i]=1;
if(i%pri[j]){
mu[i*pri[j]]=-mu[i];
g[i*pri[j]]=pri[j];
F[i*pri[j]]=1ll*F[pri[j]]*F[i]%Mod;
}
else{
mu[i*pri[j]]=0;
g[i*pri[j]]=g[i]*pri[j];
F[i*pri[j]]=g[i]!=i?1ll*F[i/g[i]]*F[g[i]*pri[j]]%Mod:1ll*F[i]*f[pri[j]]%Mod;
break;
}
}
}
for(int i=2;i<=N;i++)F[i]=(F[i-1]+F[i])%Mod;
}
int Solve(){
int ans=0,j;
for(int i=1;i<=n && i<=m;i=j+1){
j=min(n/(n/i),m/(m/i));
ans=(ans+1ll*(F[j]-F[i-1]+Mod)*(n/i)%Mod*(m/i)%Mod)%Mod;
}
return ans;
}
int main(){
freopen("4407.in","r",stdin);
freopen("4407.out","w",stdout);
scanf("%d %d",&T,&k);
Prepare();
while(T--){
scanf("%d %d",&n,&m);
printf("%d\n",Solve());
}
return 0;
}
评论 (0)
