这题我居然挂了6次……简直是耻辱啊!
dead*4:二分上界打错
dead*1:二分判断条件打错
没救了……
好了,现在说一下题解
首先我们利用二分将其转化为判定[1,x]有多少个数不是完全平方数的正整数倍
------------------------以下为懒癌发作的Lvat_s复制的PoPoQQQ的题解
然后利用容斥原理,
x以内的无平方因子数
=0个质数乘积的平方的倍数的数的数量(1的倍数)
-每个质数的平方的倍数的数的数量(9的倍数,25的倍数,...)
+每2个质数乘积的平方的倍数的数的数量(36的倍数,100的倍数,...)-...
容易发现每个乘积a前面的符号恰好是mu(a)
x以内i^2的倍数有[x/i^2]个,故有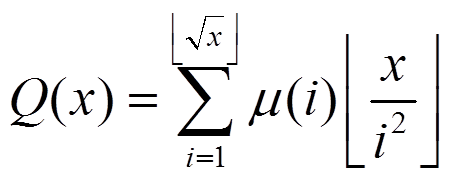
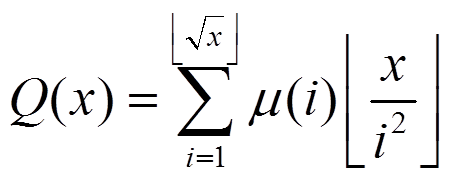
这题和莫比乌斯反演没关系,算是莫比乌斯函数的一个应用吧。。。
-------------------------------------------------------------
详情请看代码
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
long long T,k,tab[1000005],prime[1000005],mu[1000005],cnt;
void Prepare(long long Num){
mu[1]=1;
for(long long i=2;i<=Num;i++){
if(!tab[i]){
prime[++cnt]=i;
mu[i]=-1;
}
for(long long j=1;j<=cnt && i*prime[j]<=Num;j++){
tab[i*prime[j]]=1;
if(i%prime[j])mu[i*prime[j]]=-mu[i];
else {mu[i*prime[j]]=0;break;}
}
}
}
long long Test(long long x){
long long sq=(int)sqrt(x),ans=0;
for(long long i=1;i<=sq;i++){
ans+=mu[i]*(x/(i*i));
}
return ans;
}
long long Solve(long long k){
long long l=1ll,r=10000000000ll,ans=210000000000000ll;
while(l<=r){
long long mid=l+r>>1,tmp=Test(mid);
if(tmp<k){l=mid+1;}
else {ans=mid;r=mid-1;}
}
return ans;
}
int main(){
freopen("2440.in","r",stdin);
freopen("2440.out","w",stdout);
scanf("%lld",&T);
Prepare(1000000);
while(T--){
scanf("%lld",&k);
printf("%lld\n",Solve(k));
}
return 0;
}
 评论 (0)
评论 (0)