3.17
先开一坑……
计划3.27正式开始停课专心竞赛。
这到时候就用来记录一下每天被虐的经历吧。
毕竟AH不是强省,这个时候停课也够了吧。
今年我进省队希望=0
(NOIP作弊的都去死吧!你们自己作弊就算了,还让AH丢了一个名额)
预计省队名单,到时候看看估算的对不对
wzf(Newnode) lzz(C_Sunshine) cjy(YJC) wlp(JOHNKRAM) lyf(shpgy)(女队) wyx(Thaddeus) xdm(flea)
其实wyx大爷很强的……但是因为坑·卡名额估计要买C类了……
高一其他大爷也存在卡进省队的可能……但是估计希望不太大。。
我这个sb就更不用说了,进省队期望=0
NOI2017再见了。。。反正已经弃疗所以3.27再停课咯
(当然wyx大爷和shpgy两位高一之神已经停课了)
----------------------------------------------------------
3.23
大爷们去ZJOI2016了,我还在wh月考……
已经考挂了,智商不够只能拼OI了……
wyx大爷当然不用月考啦
----------------------------------------------------------
3.26
月考完挂
明天就要集训了呢。。alpq654321来讲dp。。好激动啊
----------------------------------------------------------
Day1
今天是alpq654321讲DP和BZOJ选讲。。十分资瓷啊
下午xdm成为最佳口胡选手。
“这位橙衣小哥,你来回答一下这个问题”
今天见到了bzoj上神乎其神的神犇——yyhslyz本人
当然我也在下面口胡啊……不过我当然不会作死上去讲的
----------------------------------------------------------
Day2
今天考试。
先开T1,感觉是一道数据结构好题啊,前两天看的点分治好像有点像
T2感觉是一道DP好题啊……应该和昨天上课有些关系吧
T3感觉是一道打表好题
不管了先码暴力。
T1码到9:30
T2码到10:40
T3写了一个打表程序开着跑(此时11:30)
在11:30前想了一下T1的正解,似乎树链剖分能乱搞不少分?(此时11:40)
然后开始码码码。
然后就没码完。
最后交了两暴力一个表
然后GG喽
lyz:今天感觉三题中两题要被卡常
太神了居然会正解
slx:我第一题按位树剖黑白点的
好像大家都会T1。。
中午吔饭归来,发现我好像是rank27?不过好多同分啊……还有几个同分在我上面……
wyx大爷A掉了T1太神了
gqy100 lyz140 rky120
仔细一看我T1暴力写挂了然后爆零
果然人太弱
cyd和slx没考好只有70。。默哀
下午讲题,T1是点分治好题
lzz和wyx大爷T1就用lyz乱搞做法卡常数卡过了卡常小法坏
T2果然神奇DP
T3是一个最短路+DP
感觉要好好学习一下点分治了
orz wzf 300虐场
lzz 260 故意取模不AK
wyx 160同样虐场
都好神啊orzorz
今晚的订正工作似乎比较艰辛……毕竟要学习点分治啊……
----------------------------------------------------------
Day3
今天是lh大爷讲课,被xdm大D一通
以后要换个位子了
下午的题目好难啊……我只会口胡暴力乱搞
明天考试不会考这些东西吧……(立flag)
----------------------------------------------------------
Day4
lh大爷的题目
滚粗爆炸了(0+10+0)
T1T3暴力写残
T2其实我不会凸包直接输出n有10分
高一垫底
----------------------------------------------------------
接着爆炸
看到题目就浑身不想写
最讨厌找规律了
然后t1写了暴力,但是好像忘掉了逆元怎么求?
t2打表输出
t3写了一个鬼畜贪心直接爆0(你不是在Noi Openjudge上做过这个DP吗)
然后0+10+0滚粗了
lyz T2搞了50太神了%%%
cyd T3直接AC也是很神%%%
其他人好像都考的比我好。。。
----------------------------------------------------------
Day6
wzf讲课,极其资瓷!
基本一揽子解决了数论。(但是现在又忘掉了)
----------------------------------------------------------
Day7
nxy讲课
上午可以接受,但下午太快了吧
感觉很神。。。
----------------------------------------------------------
Day8
nxy考试
15+0+30滚粗
T3居然是仙人掌
T1 T2都是找规律/乱搞
蒟蒻表示乱搞能力太差不敢做
----------------------------------------------------------
Day9-Day12
天天爆炸,上课梦游
太颓废了
(其实是懒得写了。。)
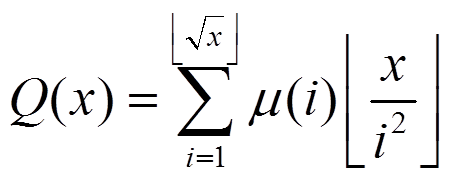


 为满足
为满足 且
且 和
和 的
的 的对数
的对数 为满足
为满足 且
且
